 |
 |
 |
|
 |
 |
 |
| |
|
PREVIOUS |
 |
NEXT |
|
|
| |
|
|
|
|
|
|
| |
|
The 3D Page Turn Algorithm |
|
|
| |
|
|
|
|
|
|
| |
|
At the core of a 3D publication is a graphical page turn that must be sharp, fluid, responsive and realistic -- a page that flows like paper when it turns. Several years’ research into page turn algorithms showed that an ideal geometric curve to describe the top and bottom edges of a turning page is is a one-quarter ellipse arc.
|
|
|
| |
|
This illustration shows a selected sequence of frames of a complete page-turn animation sequence from beginning to end. After initiating the page-turn, the reader will see a fluid turn, either forwards or backwards, to the next or previous page. Using the arc of an ellipse to bend the page gives the turning page a natural flow that mimics paper and looks totally realistic.
Rather than directly instructing the display to project a frame at a predetermined time (as other graphical page-turns do), a high-resolution timer, which marks the elapsed time from the start of the page-turn sequence, controls the animation. |
 |
|
|
| |
|
Each time the operating system loop calls for a refresh the algorithm calculates the correct position of the turning page and draws a geometrically accurate frame. This means a fluid page-turn animation can be displayed on any device, whatever the processor speed. |
|
|
| |
|
|
|
|
|
|
| |
|
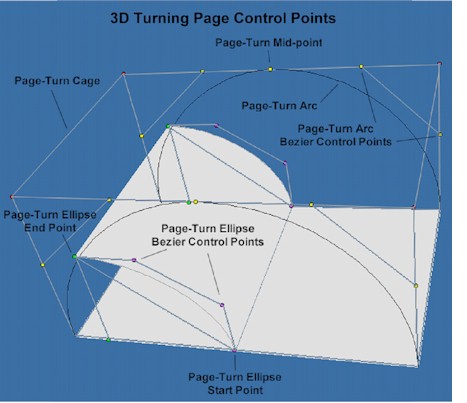 |
In this page turn algorithm an (imaginary) 3D cage is constructed around control-points calculated from the dimensions of the page. Within the cage an arc describes the path of the outer page corner points during the page-turn sequence and also represents the proportional time-line for the page-turn and provides a high precision radian value (0 to π/2) of elapsed time when the operating system display refresh loop calls for an update.
The elapsed-time value provides the critical variable for calculating the whole page-turn page turn sequence and is the key to delivering a fluid, flowing and realistic page-turn. It determines the position of the page turn end pointand the axis values of an ellipse. From here it is possible to construct a one-quarter-arc ellipse page edge. These control points are manipulated in a cubic Bezier curve equation and rotated in 3D space to the orientation and scale of the publication being viewed. |
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| |
|
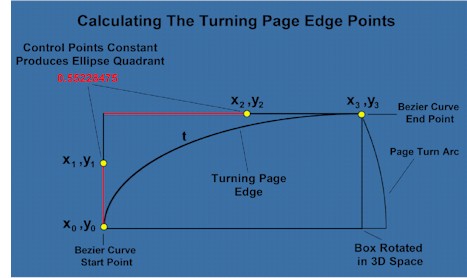
A useful property of cubic Bezier curves is that that the four x/y control points can be rotated in 3D space and translated to screen coordinates before calculating the line points. Therefore in calculating the position of the page edge, it is only necessary to calculate the rotated and translated control points and plot the page edge normally.
Using the page turn outer arc to provide a time-line and a geometric curve to bend the page is what makes the page flow naturally as it turns. Using elapsed time to control the page turn means that the number of frames displayed in a page turn sequence depends upon the device but the turning time is constant on all devices. |
 |
|
|
| |
|
|
|
|
|
|
| |
|
Once all top and bottom page edge points are known and translated to screen coordinates the turning page itself can be constructed. The page is drawn vertically in lines, which and anti-aliased to 16th of a pixel to produce smooth joining and clean edges. The contents on the pages are mapped to these lines from a laid-out page in memory. This produces a proportional and geometrically accurate transformation of the page contents to the turning page.
The actual drawing and mapping of the page-turn is done when the final display coordinates are known. The illustration below shows how a 3D turning page magazine would look face-on in mid-turn. The graphical control points are shown: |
 |
|
|
| |
|
|
|
|
|
|
| |
|
 |
|
|
| |
|
|
|
|
|
|
| |
|
NEXT - Sharp Text in a 3D Publication |
|
|
| |
|
|
|
|
|
|





